2021国际眼科临床研究大会
在广州顺利召开
PLAYBACK
视频回放入口
照片回放入口
有效期一个月
（截止2021年5月11日）
回放入口
春暖花开之际，眼科临床研究领域的年度盛宴——2021国际眼科临床研究大会于4月9-11号在中山大学中山眼科中心珠江新城院区学术报告厅隆重召开。本次大会线上线下结合，吸引了来自全国各地300多名观众线下现场参会，会场气氛热烈，座无虚席。线上更是热火朝天，截至新闻发稿前直播在线累计观看97,938人次。创历史新高，弹幕好评如潮。
2021国际眼科临床研究大会由广东省医师协会眼科医师分会主办，中山大学中山眼科中心组织承办，邀请来自美国、德国、澳大利亚、日本、韩国、新加坡等18位国际著名眼科临床研究专家云端相聚，联同国内128位顶级眼科大腕亲临现场，共同为大家奉上一场丰富多彩的眼科临床研究学术盛宴。
4月9日大会第一天，临床研究国际论坛率先拉开序幕。张秀兰、吕林教授领衔主持青光眼合并高度近视临床研究峰会，与11个国家包括中国、美国、德国、澳大利亚、日本、韩国、新加坡等顶尖青光眼和视网膜专家，就高度近视和青光眼研究进展进行深入交流。国外嘉宾包括美国哈佛大学David Friedman教授、美国约翰·霍普金斯大学Neil Bressler教授、德国海德堡大学Jost Jonas教授、韩国首尔大学医院Ki Ho Park教授、澳大利亚悉尼大学Paul Healey教授、新加坡国立眼科中心Tin Aung教授、Ching-yu Cheng教授、日本东京医科齿科大学Kyoko Ohno-Matsui教授、澳大利亚墨尔本大学何明光教授、世界青光眼学会前任主席Robert N. Weinreb教授和美国加州大学圣地亚哥分校Linda M.Zangwill教授倾情参与讨论。
4月10日，大会开幕式由中山大学中山眼科中心临床研究中心主任、大会副主席张秀兰教授主持。在简单温馨的开幕式上，以四个视频的形式，分别介绍和展示了中山眼科中心、中山眼科中心临床研究中心、出席大会的所有演讲、主持和点评嘉宾风采以及给予支持的合作伙伴。伴随悠扬的音乐、精彩的视频全场观众都注视着大屏幕，深切感受到承办方对出席专家、合作伙伴和台前幕后工作人员的感恩之心。
大会副主席、开幕式主持人张秀兰教授
广东省医师协会常务副会长吴少林为本次大会致辞，他提到2019年由广东省医师协会举办的首届国际眼科临床研究大会取得了圆满成功。经历了不平凡的2020年，我国对于新冠肺炎疫情的有效控制，让我们今天能有机会再次举办国际眼科临床研究大会。他嘱咐大家要珍惜面对面的学习机会，相互促进，共同进步。
广东省医师协会吴少林常务副会长
大会名誉主席、广东省医师协会眼科医师分会会长余敏斌教授发表致辞，对所有莅临演讲的国内外嘉宾以及组织者的辛勤付出表示衷心的感谢。他热切期望眼科人在本次会议，有所收获，在眼科临床研究的大道上继续奋力前行。
大会名誉主席、广东省医师协会眼科医师分会会长余敏斌教授
大会主席、中山大学中山眼科中心主任刘奕志院长首先对所有与会专家和学者表示热烈欢迎。他在致辞中分享了自己从事临床研究中的经验和心得，强调临床研究是深奥的学问，光有热情是不够的，最迫切的是要提高临床研究水平，最后期望在场的学者和线上的所有观众，都可以在这场学术盛宴中共同提高，共享眼科临床研究发展的累累硕果。
大会主席、中山大学中山眼科中心主任
刘奕志院长
中华医学会眼科学分会候任主任委员孙兴怀教授致辞：他坦言作为医生、研究者的终极目标是服务患者，服务人类，得到科学合理的方案，保障民众视觉健康，临床研究不可或缺，期望大家更关注临床研究。他强调本次临床研究大会的必要性，希望大家认真学习。
中华医学会眼科分会候任主任委员孙兴怀教授
中国医师协会眼科分会会长王宁利教授高度肯定了本次眼科临床研究大会举办的必要性，他表扬本届会议组织有方、内容丰富、专家云集、学科交叉激情碰撞、交流形式多样，将是一场精彩美妙的学术会议。
中国医师协会眼科分会会长王宁利教授
伴随着悠扬音乐，开幕式在温馨合照留影后结束，眼科学领域、临床研究领域等精英大腕共聚一堂，留下珍贵美好的回忆。
精彩紧凑的学术日程接踵而至，上午第二时段是Keynote speech主旨演讲，由葛坚、余敏斌、林浩添教授主持，澳门科技大学张康教授和新加坡国立眼科中心Tien Yin Wong教授带领大家穿越眼科人工智能的过去、现在、未来。深度阐述将大数据、人工智能转化为更好的医疗作用，为人类做出贡献。两位科学家的演讲题目分别是“Translating big data, AI and drug discovery into better healthcare delivery and therapies”和“AI and digital Ophthalmology: past, present and future”，精彩报告给在座和线上的观众带来深邃的思考和启发，引领医疗信息科技发展。
新加坡国立眼科中心Tien Yin Wong教授
上午第三时段是临床研究大师论坛（一），论坛由林晓峰、曾骏文、张清炯教授主持。首都医科大学附属北京同仁医院王宁利教授、复旦大学附属眼耳鼻喉科医院孙兴怀教授、上海交通大学范先群教授、美国德克萨斯A&M大学健康科学中心Leng Han教授、Ophthalmology主编加州大学三藩市分校Stephen McLeod教授分别呈上：“临床问题驱动的科学研究”、“临床青光眼神经损害诊断结构与功能、孰优？”、“眼恶性肿瘤关键治疗技术建立和应用研究”、“Maximizing the Utility of Omics Data for Precision Medicine”、“Thinner vs Thinnest: Clinical Outcomes of DSAEK vs DMEK”。大咖们围绕各自研究领域的临床科研成果演讲，彰显权威专家的学术水平。
上海交通大学范先群教授
美国德克萨斯A&M大学健康科学中心Leng Han教授
Ophthalmology主编Stephen McLeod教授
大师云集的临床研究论坛一场怎么够?大会贴心准备了临床研究大师论坛 （二）。由卓业鸿、梁小玲、陆晓和教授主持。何氏眼科医院何伟教授、天津医科大学眼科医院李筱荣教授、浙江大学医学院附属邵逸夫医院姚玉峰教授、北京大学第一医院杨柳教授、世界青光眼学会前任主席美国圣地亚哥Shiley眼科研究所Robert N. Weinreb教授等专家为大家逐一呈上“临床医学转化中心的价值创造”、“康柏西普眼用注射液在真实临床实践中的长期安全性及疗效研究”、“术中OCT监测飞秒激光辅助的姚氏法深板层角膜移植术”、“从葡萄膜炎影像中发现研究兴趣”、“Personalizing Glaucoma with 24 Hours Intraocular Pressure”五个精彩讲题，赢得现场观众阵阵热烈掌声。
北京大学第一医院杨柳教授
世界青光眼学会前任主席美国圣地亚哥Shiley眼科研究所Robert N. Weinreb教授
接下来是广受欢迎的经典环节临床研究新手术、疑难手术视频展示。由张良、张少冲、晏世刚教授担任主持。马进、李莹、张秀兰、赖一凡、袁钊辉、沙翔垠、颜建华、祁勇军、张淳等教授展示了炉火纯青眼科手术实战技巧。他们带来精彩报告“眼内血管瘤玻璃体手术的反思”、“SMILE操作技巧”、“青光眼微创手术GSL-KBD-TMH-GATT手术操作与技巧”、“玻璃体视网膜-白内障联合手术”、“一种新颖的经角巩缘的人工晶状体缝线固定术”、“外伤性角膜血染合并视网膜脱离的手术治疗”、“甲状腺相关眼病斜视的手术”、“拨开迷雾捉秋虫----一例特殊的后极性白内障”、“术中OCT导航黄斑手术”。本专题特别邀请吴明星、杨华胜、余克明、李东豪、龙崇德、邓大明等教授担任点评嘉宾。精湛的手术技巧与专家讨论点评为观众奉上手术实践双重大礼。
任何学科都不可能孤立存在，眼科临床研究与其他学科之间的交叉碰撞尤为重要。大会进入第六时段交叉学科临床研究翘楚。由袁进、柳夏林、赵岐教授主持。广东省人民医院院长吴一龙教授、南方医科大学南方医院副院长李国新教授、南方医科大学珠江医院临床研究中心执行主任丁长海、北京同仁医院副院长魏文斌教授、北京协和医院眼科主任陈有信教授、为我们奉献“新英格兰医学杂志背后的故事”、“外科临床研究线路图”、“临床研究路线图：从观察性研究到临床试验”、“AI与5G赋能眼科临床诊疗的初步探索”、“眼内肿瘤的诊断思维”等精彩讲题。跨学科的临床研究经典案例令观众叹为观止。
右一：李国新教授，右二：陈有信教授，右三：魏文斌教授
接下来是眼科临床研究新产品、新技术、新药物汇萃时段，由金陈进、郑永欣、钟敬祥教授主持。党光福、许言午、张雄泽、张广斌、刘晓岸、袁进、杨文利、梁小玲、刘锟、吴明星、黄晶晶等教授及各位老师分享诊疗新技术在临床和科研中的应用成果。他们的报告题目分别是：“360粘小管切开术手术操作与技巧”、“超广角眼底影像新进展”、“面向真实世界应用的鲁棒AI眼底筛查产品与技术”、“最新连续视程人工晶体应用”、“微创青光眼手术新利器—PRESERFLO青光眼引流器”、“眼部疾病抗过敏治疗新策略”、“最新扫频源前节CASIA OCT在眼科的应用”、“最新扫频源OCT在眼底疾病中的应用”、“更小分子新一代抗VEGF药物--倍优适临床应用新进展”、“白内障手术后的视觉质量评估”和“青光眼药物的研发与未来”。
周六下午压轴登场的是国际临床研究热点大师论坛，连线邀请了Lancet Digital Health主编Rupa Sarkar教授、新加坡国立眼科中心Daniel Ting教授、日本东京医科齿科大学Kyoko Ohno-Matsui教授、韩国首尔国立大学Ki Ho Park教授、德国海德堡大学Jost Jonas教授、澳大利亚墨尔本大学Mingguang He教授等六位知名专家。林浩添、张秀兰教授现场主持，与国际知名主编、国际多中心PI共聚云端，联合呈现一场精彩的线上专题。现场观众提问踊跃，直播留言赞美不断。线上线下的学者纷纷表示受益匪浅。
Daniel Ting：AI and Digital Innovation in Ophthalmology during COVID-19
Kyoko Ohno-Matsui：Imaging of posterior staphyloma in pathologic myopia
Jost Jonas：Myopia: Anatomy, clinics and aspects of its etiology
Mingguang He：Investigator initiated clinical research: from design to publication
Rupa Sarkar：Publishing in The Lancet Digital Health
Ki Ho Park：Ten-Year-and-Beyond Longitudinal Change of ß-Zone Parapapillary Atrophy: Comparison of POAG with Normal Eyes
大会来到了第三天，为了表达对授课嘉宾的感恩之心，大会再次播放了所有参会嘉宾介绍视频。第一时段是临床研究信息化、项目开展运行与管理专题，由林明楷、张铭志教授主持，中山大学中山眼科中心张秀兰教授、林浩添教授、罗燕教授、刘玉红老师，广州翔康医疗器械技术服务有限公司易敏老师、上海砝码斯医药生物科技有限公司霍春华老师从“EDC平台在高质量科研项目开展中的应用”、“如何申请AI医疗器械临床试验项目”、“如何进行干细胞临床研究项目备案”、“CRO在临床研究中的作用”、“架起临床研究的桥梁—研究护士/研究协调员角色的崛起”、“SMO临床协调员在临床研究中的作用”等展开精彩演讲，这个专题为在场学者介绍了临床研究信息化、项目运行管理等流程、注意事项，实用性强。
实践是检验真理的唯一标准，临床研究必须从实践出发。大会特设专题临床研究与循证实践，由郑永欣、林小铭、侯光辉教授主持，中国人民解放军总医院王丽强教授、北京同仁医院张丰菊教授、汕头国际眼科中心陈浩宇教授、中山眼科中心罗莉霞、梁丹、文峰教授为大家分别呈上“BostonII型人工角膜治疗难治性角膜盲”、“术中OCT实时动态观察白内障手术中切口相关角膜后弹力层脱离的临床研究”、“角膜生物力学在圆锥角膜筛查中的作用”、“角膜穿通伤的队列研究”、“如何将临床问题提升为临床研究”、“如何揭示一种新临床征象的思辨”等精彩课题。六位经验丰富的眼科专家为大家讲述从临床到临床研究的实践过程，推心置腹，以启后人。
接下来是临床研究方案与设计案例实战分析专题，由李涛、卢蓉、吴开力、汪建涛教授主持，邀请的演讲者都是来自全国各地临床研究做得十分优秀的青年才俊。中山眼科中心李飞、王伟，中山大学附属第一医院彭振维、庄晓东，北京同仁医院乔春艳、中山大学孙逸仙纪念医院陈凯、中山大学肿瘤防治中心唐林泉等担任演讲嘉宾，围绕临床研究方案等方方面面，结合个人临床研究经历进行深度讲解，他们的精彩报告分别是“AI及大数据临床研究”、“从临床到研究”、“双眼对称性分析在青光眼和糖尿病视网膜病变中的诊断价值”、“资源有限型医院如何开展改变临床实践的研究”、“注册研究”、“队列研究”、“基于数据解析临床问题的ABC：Association，Biology，Causation”。同时邀请黄丹平、杨晓、蓝育青、甘小亮、杨晖、张健等教授和统计师担任点评嘉宾。青年才俊们演讲精彩、点评到位，全场多次响起雷鸣般的掌声。
大会为青年科学家提供展示平台---青年科学家论坛，由中山眼科中心郑丹莹、梁凌毅、杨扬帆教授主持。周世有、毛羽翔、何丽文、李劲嵘、刘炳乾教授和金玲统计师担任点评嘉宾。中山眼科中心陈士达、靳光明、李治玺、于珊珊、李松珊、刘耀明，中山大学肿瘤防治中心张媛、刘需，温州医科大学附属眼视光医院张绍丹，复旦大学附属眼耳鼻喉科医院戴毅等后起之秀作专题汇报。青年科学家展示了各自的优秀研究结果，以及在疾病诊疗研究上新颖的见解。江山代有才人出，期待青年学者在临床研究领域大发光彩。
临床研究方法与设计培训班是大会特别设计的时段，在4月9日（周五）大会第一天下午进行。由中山眼科中心临床研究中心副主任陈翔主持，特别邀请了北京大学第一医院姚晨教授、中山大学肿瘤防治中心李济宾研究员、南方医科大学珠江医院朱兆华副研究员、福安易数据技术（天津）有限公司首席科学家洪松林教授、中山大学徐琳教授为大家献上“如何利用真实世界数据进行临床研究”、“干预性临床研究中的常见统计学问题”、“如何写好一篇临床研究文章”、“真实世界驱动的临床研究创新与实践”、“孟德尔随机化在临床研究中的应用”等精彩报告。培训班线上线下非常爆满，超过了预期，说明大家都非常渴望在临床研究方法学上得到提高。
有朋自远方来，2021国际眼科临床研究大会除了安排丰富精彩课题日程，还贴心为每一位来到中山眼科中心的所有演讲、主持、点评嘉宾、客人安排参观眼科学馆、国家眼科重点实验室、临床楼门诊部、住院病房、临床研究中心。所有来宾都表扬大会的周到用心，同时赞叹中山眼科中心不愧是全国最好的眼科医院，院区布局精致温馨，设备先进齐全，人才济济，是患者之福。
2021国际眼科临床研究大会接近尾声，张秀兰教授主持闭幕式。她在闭幕式中由衷地感谢广东省医师协会眼科医师分会的协助，感谢中山眼科中心领导的大力支持，感谢所有国际国内的演讲嘉宾和点评专家，感谢所有线上线下的同道朋友，感谢所有支持大会战略合作伙伴，感谢台前幕后所有工作人员的辛勤付出。让我们一起共同期待，明年再次相聚！
PLAYBACK
视频回放入口
照片回放入口
有效期一个月（截止2021年5月11日）
中山眼科中心临床研究中心
获取最新研究资讯
了解最新政策信息
掌握最新机构动态
推送最新受试招募
---来源：临床研究中心---
---编辑：郭燕婷、窦明玥、王贞玉---
---审核：陈翔---
---审定：张秀兰---
继PSM方法之后，我们一起来学习多重检验。多重检验的问题在临床研究中并不少见。研究中若具有多个研究终点、需要比较不同治疗组间的差异、分析多个结果以及对同一结果在不同时间的多次分析等，都需要进行多重检验，然而多次的假设检验会增大犯Ⅰ类错误的风险，从而导致试验结果的不准确性[1]。只有部分文章在多重检验中进行校正以减少Ⅰ类错误的概率，且大部分作者没有说明进行校正的理由。多重检验是较复杂的统计学问题，这里尝试简单地解释其中的基本原理。
（图片来自BMJ 1998）
总体错误率
当在单个的假设检验中，我们会预先确定好显著性水平α（通常取0.05），这是在此次检验中会得到假阳性结果的风险，以便控制好Ⅰ类错误的发生概率。换句话来说，研究者会控制单次检验中可能出现假阳性结果的概率在5%。
与单个假设检验类似，若同时检验多个假设时，控制好Ⅰ类错误的概率也是主要的任务。举个例子，研究中有k个假设，每个假设都是相互独立的，显著性水平是α，那就意味着如果进行k次假设检验，那么不犯Ⅰ类错误的概率是（1-α）k，则至少犯一次Ⅰ类错误的概率是1-（1-α）k。而总体错误率（familywise error rate, FWER）也指的是1-（1-α）k。而且当k不断增加，（1-α）k趋向于0，1-（1-α）k趋向于1，所以我们必须通过多重检验校正控制Ⅰ类错误的发生。
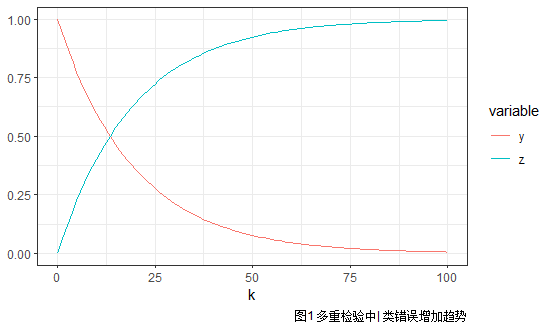（图1：当α=0.05时，y=（1-0.05）k，z=1-（1-0.05）k。随着k的增加，y和z发生变化。）
为了使FWER达到0.05，那么每次多重检验中显著性水平都必须低于0.05，即1-（1-α）k中的α低于0.05。而Bonferroni校正就是通过调整显著性水平来控制多重检验中犯I类错误的概率，公式为α’=α/k。
进行多重检验校正的情况
2.1 多个治疗组
随机对照试验中通常会设置多个试验组与对照组进行比较，意味着要在多组试验组之间要进行多次比较，同时也要考虑不同干预之间的交互作用，那么这时候可能需要考虑多重检验校正，以避免Ⅰ类错误的增加。
2.2 亚组分析
临床试验中除了对不同干预手段进行分组外，还可以根据性别、年龄、是否存在合并症或疾病严重程度进行分组，以确定总体试验结果是否适用于所有符合条件的患者，或者不同分组间的干预效果是否存在差异，因此需要考虑多重检验校正。
2.3 相同结果的重复测量
在不同时间重复检验相同结果也会增加犯Ⅰ类错误的风险。临床研究中，通常在不同治疗组中对受试人群按照一定的时间间隔进行重复测量，目的是观察不同治疗方式随时间变化的趋势。对于不同治疗组，研究者反复测量血压、药物清除率、抑郁或疼痛评分等结局时，注意多重检验造成Ⅰ类错误的增加。
2.4 多个研究结局
临床试验通常是通过评估多种研究结局（或“研究终点”）来判断试验的效果。例如在心血管试验中，感兴趣的结局可能包括住院、中风、心力衰竭、心肌梗塞、心脏骤停、残疾和死亡。如果我们以5%的显著性水平分别检验每个研究结局，那么FWER会高于5%，此时应调整分析方案。
2.5 多次中期分析
在临床研究中通常需要进行长期监测，即在不同的时间对同一结局进行多次分析，目的是为了确定是否提前终止试验，出现的原因可能是新的治疗方法与对照组之间存在显著差异或造成严重的不良事件。进行多次分析需要对各阶段积累的数据进行反复比较，从而增加了犯Ⅰ类错误的风险。
2.6 探索性研究和验证性研究
验证性研究（如随机对照试验）是检验预先确定的关键假设，需要确定合适的样本量进行数据收集和分析，必要时需进行多重检验校正，为研究提供有效可信的证据。而探索性研究（如观察性研究、Ⅰ期或Ⅱ期临床试验早期）是进行新干预措施之前的早期研究，可以说是发现假设的一个过程，探索性研究的结果后期需要进行验证性研究进一步检验，因此，探索性研究不要求进行多重检验校正。
多重检验校正的方法
多重检验校正有很多种方法。其中最简单，最经典的方法是基于P值的Bonferroni校正。在此方法中，每次检验的显著性水平都是α/ k，其中k是检验次数，α指的是原先的显著性水平，这样可以保证这一组假设总体犯Ⅰ类错误的风险在α之内。然而，Bonferroni校正总是以牺牲检验效能（1-β）来保证FWER，此时若要维持Ⅱ类错误在合理的水平，就需要增加样本量[2]。
此外，Benjamini-Hochberg（简称BH）也是多重检验校正的基本方法，而此方法是基于错误发现率（false discovery rate, FDR）基础上的控制方法[3]。FDR指的是多重检验中错误拒绝原假设（拒绝真的原假设，即犯Ⅰ类错误）的个数占所有被拒绝的原假设个数的比例的期望值，像FWER一样，是另外一种衡量多重检验中可能犯Ⅰ类错误概率的方法。BH法过程较复杂，步骤如下：（1）将原始m个P值升序排序，排序后表示为P1、P2……Pm；（2）（i / m）*q计算每个P值的BH临界值，其中i是P值等级，m是检验次数，q是FDR（自由取值，通常≤0.05）；（3）排序后的P值与BH值进行比较，找到小于或等于临界值的最大原始P值，此时对应排序等级为J，记为PJ，则PJ ≤（J/m）*q；（4）拒绝所有等级在PJ之前及PJ（即1≤i≤J）对应的原假设，接受这些原假设对应的备择假设，即认为差异具有统计学意义[3]。
表1：Benjamini-Hochberg法、Bonferroni法校正后及未校正前的多重检验（m=10，FDR=q=0.05，α=0.05）
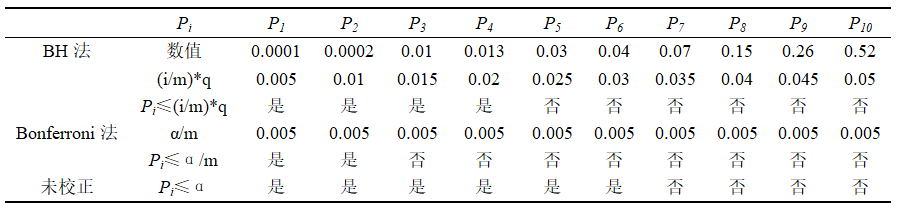
其中，“是”表示拒绝原假设，“否”表示不拒绝原假设；i/m*q 表示BH临界值，P4=0.013就是我们寻找的PJ。
实际上，BH法相当于对排序后的假设重新确定了不同的显著性水平（实际上相当于临界值），随着等级i的不断增加，重新确定的显著性水平（临界值）也不断增加[4]。相对于Bonferroni法中显著性水平一直是α/k来说，BH法拒接原假设的标准显得不过于保守。这样就能从统计学上保证FDR不超过α，从而保证多重检验整体犯I类错误的概率低于预先设定的显著性水平α。
结语
虽然两种方法都是用于多重检验中控制Ⅰ类错误的发生，但两者之间仍有区别。Bonferroni校正方法虽简单，但过于严格，灵敏度不高，难以比较出不同组别之间的差异；用于控制FDR的BH方法会基于每个P值进行校正，显得更加灵活，且提高了检验效能。实际上，多重检验问题会存在不同的复杂情况，如研究方案中多个治疗组、多个研究结局和多次中期分析并存等，那么多重检验校正就更具有挑战性，简单的Bonferroni和BH方法并不能解决问题，需要更复杂的统计方法[5]。
当研究者发表研究结果时，为了保持统计结果与结论的一致性以避免误导读者，应该清楚地认识多重检验校正的重要性，并应解释校正的原因。
